Obsah
- 1 4 způsoby, jak lhát pomocí statistik
- 2 [upravit | upravit kód]
- 3 Vzorek je ze své podstaty zaujatý [ upravit | upravit kód]
- 4 Dobře zvolený průměr [ editovat | upravit kód]
- 5 Nuance, o kterých se skromně mlčí [editovat | upravit kód]
- 6 Mnoho povyku téměř pro nic [edit | upravit kód]
- 7 Harmonogram nemůže být lepší [upravit | upravit kód]
- 8 Schematický obrázek [upravit | upravit kód]
- 9 Pseudopodložená figura [upravit | upravit kód]
- 10 Opět „po znamená jako výsledek“ [upravit | upravit kód]
- 11 Jak vytvořit statistiku [ upravit | upravit kód]
- 12 Jak umístit statistiky na jejich místo [upravit | upravit kód]
- 13 Vydání v jiných jazycích [ upravit | upravit kód]
- 14 V ruštině [upravit | upravit kód]
- 15 Poznámky [upravit | upravit kód]
- 16 Jak správně lhát pomocí statistik
- 17 Vzorkování zkreslení
- 18 Výběr správného průměru (Dobře zvolený průměr)
- 19 A 10 dalších neúspěšných experimentů, o kterých jsme nepsali
- 20 Hraní si s měřítkem
- 21 Vyberte 100 %
- 22 Skrytí požadovaných čísel
- 23 Vizuální metafora
- 24 Příklad kvalitní vizualizace
- 25 Závěr a další čtení
4 způsoby, jak lhát pomocí statistik
Jak lhát pomocí statistik je kniha, kterou napsal Darell Huff v roce 1954. Hovoří o různých způsobech, jak lze statistiky použít k oklamání publika a manipulaci s jejich názory. Uvažuje se o mnoha konkrétních příkladech, především z amerického života (reklama, politika, propaganda a agitace).
Kniha je určena pro laického čtenáře a je vybavena pestrými ilustracemi. Materiál je podán názorně a přístupnou formou, což knize zajistilo vysokou oblibu – jde o jednu z největších publikací o statistice druhé poloviny 1. století [XNUMX].
[upravit | upravit kód]
Vzorek je ze své podstaty zaujatý [ upravit | upravit kód]
Vysvětlení, co je to sampling a jak tazatelé nevědomky vybírají respondenty a ovlivňují jejich odpovědi.
Dobře zvolený průměr [ editovat | upravit kód]
- Aritmetický průměr
- Medián
- Móda
Příklady ukazují, jak volba typu průměru ovlivňuje jeho hodnotu pro stejné vzorky. Upozorňuje se na možnost manipulace nepřipraveného čtenáře volbou „pohodlného“ (pro manipulátora) typu průměru.
Nuance, o kterých se skromně mlčí [editovat | upravit kód]
V této kapitole autor zkoumá důležité nuance statistického výzkumu, které jsou často záměrně či nevědomky ponechány bez zprávy v článcích určených široké veřejnosti.
Je vysvětlena důležitost velikosti vzorku a její vztah k typu populace. Jsou uvedeny příklady manipulace s velikostí vzorku:
- Testování účinnosti zubní pasty. Probíhají laboratorní testy účinku používání zubní pasty na šesti subjektech. Někdy se provádí série takových studií a studie, která ukazuje výsledek výhodný pro zákazníka (výrobce pasty), se používá v reklamních kampaních.
- Test vakcíny proti obrně. Očkováno bylo 450 dětí, neočkovaných 680 (kontrolní skupina). Brzy poté došlo v oblasti k epidemii, u očkovaných dětí nebyl zaznamenán jediný případ infekce dětské obrny. Ani jeden z členů kontrolní skupiny. Experiment byl od samého začátku zbaven smyslu kvůli špatné volbě počtu účastníků, protože v takto velké skupině nelze očekávat více než dva případy infekce.
- Statistická významnost
- Interval spolehlivosti
- Pravděpodobnost spolehlivosti
Na příkladu Hesselovy vývojové škály je popsáno nebezpečí vnímání bodového (mimo intervalového) hodnocení průměrné hodnoty – rodiče začnou panikařit, pokud jejich dítě neodpovídá normě (průměrné hodnotě).
Je třeba upozornit na důležitost formulací v článcích založených na statistikách. Za příklad je považováno prohlášení elektrárenských společností (1948): „Elektřina k dispozici více než 3/4 amerických farem.“ Slovo „dostupný“, které není v prohlášení nijak definováno, ztrácí význam – obvykle znamená, že elektrické vedení se nachází 10–100 mil (16–160 km) od farmy, ale dostupnost může také něco znamenat jiný. Autor také poznamenává, že při interpretaci stejných dat by bylo možné klást opačný důraz napsáním: „Elektřina není dostupná čtvrtině amerických farem.“
Kapitola končí připomenutím důležitosti čísel v grafech – graf růstu zisků společnosti za několik let (uveřejněný v časopise Fortune) čtenáři nic neřekne, protože na ose y chybí číselná označení. Z takového grafu nelze poznat, zda byl růst zisku významný, průměrný nebo blízký nule.
Mnoho povyku téměř pro nic [edit | upravit kód]
Koncepty intervalu spolehlivosti a pravděpodobnosti spolehlivosti jsou ilustrovány na příkladech ze skutečného života:
- Rozdíl ve výsledcích IQ testu mezi 98 a 101 nám neumožňuje říci, který ze subjektů má vyšší IQ, jak je patrné z úplných výsledků testu: 98 ± 3 a 101 ± 3.
- Měření obsahu škodlivých látek v různých značkách cigaret odhalilo absenci jakéhokoli významného rozdílu mezi nimi. Jedna ze značek však skončila v obsahu škodlivých látek na posledním místě (byť se zanedbatelnou rezervou z prvního místa!). Výrobce těchto cigaret (Old Gold) spustil reklamní kampaň, ve které tvrdil, že cigarety Old Gold obsahují podle nezávislé laboratoře nejméně škodlivých látek.
Harmonogram nemůže být lepší [upravit | upravit kód]
První z kapitol je věnována úvahám o metodách manipulace s využitím grafických informací.
Zvažuje způsoby, jak zkreslit vnímání grafů:
- „Komprese“ části souřadnicové sítě, údajně za účelem úspory místa. Ve skutečnosti to vede k potížím s vnímáním měřítka
Plná verze grafu
„Komprese“ části souřadnicové sítě
- Změna měřítka podél úseček a pořadnic. Tato metoda umožňuje „přeměnit“ (vizuálně) růst, který se blíží nule, na výrazný stabilní. Jako příklad je uveden graf růstu státních dotací uvedený v jednom z oznámení. Nárůst byl jen 4 %, ale vizuálně to vypadalo na téměř 400 % kvůli nárůstu měřítka podél osy y.
Schematický obrázek [upravit | upravit kód]
Diskutuje o způsobech, jak oklamat publikum pomocí infografiky.
Použití grafických objektů spojených s prezentovanými informacemi otevírá široké možnosti zneužití. Toto tvrzení je ilustrováno řadou příkladů:
- Chcete-li porovnat dva platy, můžete použít infografiku a vylosovat dva pytle peněz. Pokud je druhý plat dvakrát vyšší než první, pak bude druhý pytel nejen vyšší, ale také dvakrát širší (což je nutné pro zachování poměru). A protože je taška trojrozměrný objekt, bude obrys druhé tašky dvakrát silnější než první. Výsledkem je, že naše vidění vnímá druhou tašku jako tašku 8 (ne 2!) krát větší než první. Tuto techniku použil časopis Newsweek.
- Reklama pro American Steel and Alloy Institute pomocí infografiky ukazovala nárůst výroby oceli mezi lety 1930 a 1940 o 4.25 milionu tun (z 10 milionů na 14,25 milionů). Infografická technika (k dříve diskutovaným metodám bylo přidáno záměrné zkreslení proporcí) vedla k tomu, že naznačené zvýšení natavení bylo vizuálně vnímáno jako 1500 %. Autor poznamenává, že to je případ, kdy se „aritmetika změní ve fantazii“.
- Použití obrázků krav různých velikostí k zobrazení různých výnosů mléka v průběhu let. Kromě již diskutovaných účinků vede tato metoda k dalšímu nedorozumění – čtenář si může myslet, že je vyšší nejen dojivost, ale i větší krávy.
Obrázek níže ukazuje příklad zneužití infografiky – druhý objekt je vizuálně 8x větší:

Pseudopodložená figura [upravit | upravit kód]
Kapitola začíná žíravým doporučením: „Pokud nemůžete dokázat, co chcete, ukažte něco jiného a tvrdte, že tyto věci jsou stejné.
Existuje mnoho příkladů takových podvodů. Zejména:
- Vydání ankety názory lidí o rovných příležitostech pro bělochy a Afroameričany získat práci na základě reálné situace na trhu práce. Tento průzkum může ukázat lepší výsledky, čím více lidí s rasovými předsudky vůči Afroameričanům se ho účastní, protože takoví respondenti mají tendenci věřit, že na trhu práce neexistuje rasová diskriminace.
- Reklama na cigarety použila následující argument: „Více než 27 % velkého vzorku známých lékařů kouří hrdla, což je nejvyšší procento ze všech značek cigaret.“ Reklama implicitně naznačovala, že lékaři věděli něco zvláštního, pro ostatní neznámého, o škodách způsobených různými značkami cigaret. Ale to není pravda.
- Reklamy na odšťavňovač tvrdily, že laboratorní testy ukázaly, že extrahoval o 26 % více šťávy. Když byla položena otázka „co je co?“, dostala odpověď: „než ruční odšťavňovač.“ I když je původní tvrzení pravdivé, neumožňuje porovnávat inzerovaný produkt s produkty konkurence. Je sice nejhorší na trhu, ale přesto je o 26 % lepší než ruční odšťavňovač, pokud jde o účinnost extrakce.
- Námořní úmrtnost během španělsko-americké války byla 0,09%. U civilistů v New Yorku ve stejném období to bylo 0,16 %. Námořnictvo použilo tyto údaje ke kampani na vojenskou službu. Srovnávat tyto ukazatele je ale nesprávné – námořnictvo rekrutuje mladé a zdravé lidi, zatímco civilní obyvatelstvo zahrnuje kojence, staré lidi a nemocné.
Opět „po znamená jako výsledek“ [upravit | upravit kód]
Tato kapitola představuje koncept korelace a běžné záměny mezi příčinou a následkem. Pokud se jevy A a B vyskytují společně, lze to vysvětlit třemi způsoby:
- Událost A je důsledkem události B
- Událost B je důsledkem události A
- Jevy A a B jsou důsledkem jiného jevu/jevu
Je uvedena řada příkladů chybných úsudků o vztazích příčiny a následku. Zejména:
- Studie ukázaly, že studenti, kteří kouří, mají vyšší pravděpodobnost horších výsledků než nekuřáci. Tato skutečnost byla využita v protitabákové kampani. Z tohoto výsledku však nelze usuzovat, že kouření má negativní vliv na schopnosti žáků. Je možné, že studenti začali kouřit kvůli špatným studijním výsledkům, nebo se špatně učí a kouří z nějakého třetího důvodu (například obtížné životní podmínky).
- Výzkum ukazuje pozitivní korelaci mezi dosaženým vzděláním a příjmem. Z této skutečnosti nelze usuzovat, že pokud Vy (Váš syn, dcera atd.) získáte vyšší vzdělání, pak budou mít jistě a nutně vyšší příjem, než kdyby jej nedostávali. Tato korelace navíc neumožňuje dospět jako obecné pravidlo k závěru, že k vyšším příjmům vede právě vyšší vzdělání – ti, kteří jej dostávají, možná pocházejí z bohatých rodin, a proto mají v dospělosti vyšší příjem. Zde je příklad post hoc chyby Viz také Logické chyby.
- Studie 1500 typických absolventů vysokých škol středního věku zjistila, že 93 % mužů bylo ženatých (ve srovnání s 83 % běžné populace), zatímco pouze 65 % žen bylo vdaných. Z toho se usuzuje, že vzdělaná žena se méně pravděpodobně vdá než nevzdělaná. Studie však neukazuje vztah příčiny a účinku mezi těmito jevy. Možná by tyto neprovdané ženy zůstaly neprovdané, i kdyby nevystudovaly univerzitu.
Kapitola končí téměř neoficiálním (ale skutečným) příkladem záměny příčiny a následku mezi domorodci z Nových Hebrid. Věřili, že přítomnost vší vede ke zdraví. Tento závěr byl učiněn na základě toho, že nemocný člověk ztratil vši (protože kvůli zvýšené tělesné teplotě se pro něj životní podmínky staly nepohodlnými), zatímco všichni zdraví lidé je měli (jinými slovy, existovala pozitivní korelace mezi zdravím a přítomnost vší).
Jak vytvořit statistiku [ upravit | upravit kód]
Statistiky jsou statistické manipulace. V této kapitole autor opět na konkrétních příkladech ukazuje způsoby manipulace se statistickými daty. Vyzývá však k tomu, abychom statistická data hromadně neodmítali, ale promyšleně, důkladně a s opatrnou nedůvěrou je prostudovali, než je vezmeme v úvahu.
Jak umístit statistiky na jejich místo [upravit | upravit kód]
Autor navrhuje zkontrolovat statistiku pomocí pěti jednoduchých otázek:
- Kdo je tam?
- Jak to ví?
- Co chybí?
- Je předmět studia nahrazen?
- Dává to smysl?
Vydání v jiných jazycích [ upravit | upravit kód]
tento článek popisuje situaci ve vztahu pouze k jednomu regionu, možná porušení pravidlo o vyvážené prezentaci.
Ruviki můžete pomoci přidáním informací pro jiné země a regiony.
V ruštině [upravit | upravit kód]
- Darell Huff. Jak lhát se statistikou. – M.: Alpina Publisher, 2015. – 163 s. — ISBN 978-5-9614-5212-9.
Poznámky [upravit | upravit kód]
- ↑ „Za posledních padesát let se knihy Jak lhát se statistikou prodalo více výtisků než jakéhokoli jiného statistického textu.“ J. M. Steele. „Darrell Huff a padesát let Jak lhát se statistikouWayback Machine. Statistické vědy, 20 (3), 2005, 205-209.
Jak správně lhát pomocí statistik
Existuje takový úžasný žánr – „špatná rada“, ve které jsou dětem poskytovány rady, a děti, jak víte, dělají všechno naopak a všechno je v pořádku. Možná se totéž stane se vším ostatním?
Statistiky, infografika, velká data, analýza dat a věda o datech – tím je teď každý zaneprázdněn. Tohle všechno správně ví každý, zbývá jen, aby někdo napsal, jak se to NEDĚLÁ. V tomto článku to uděláme.
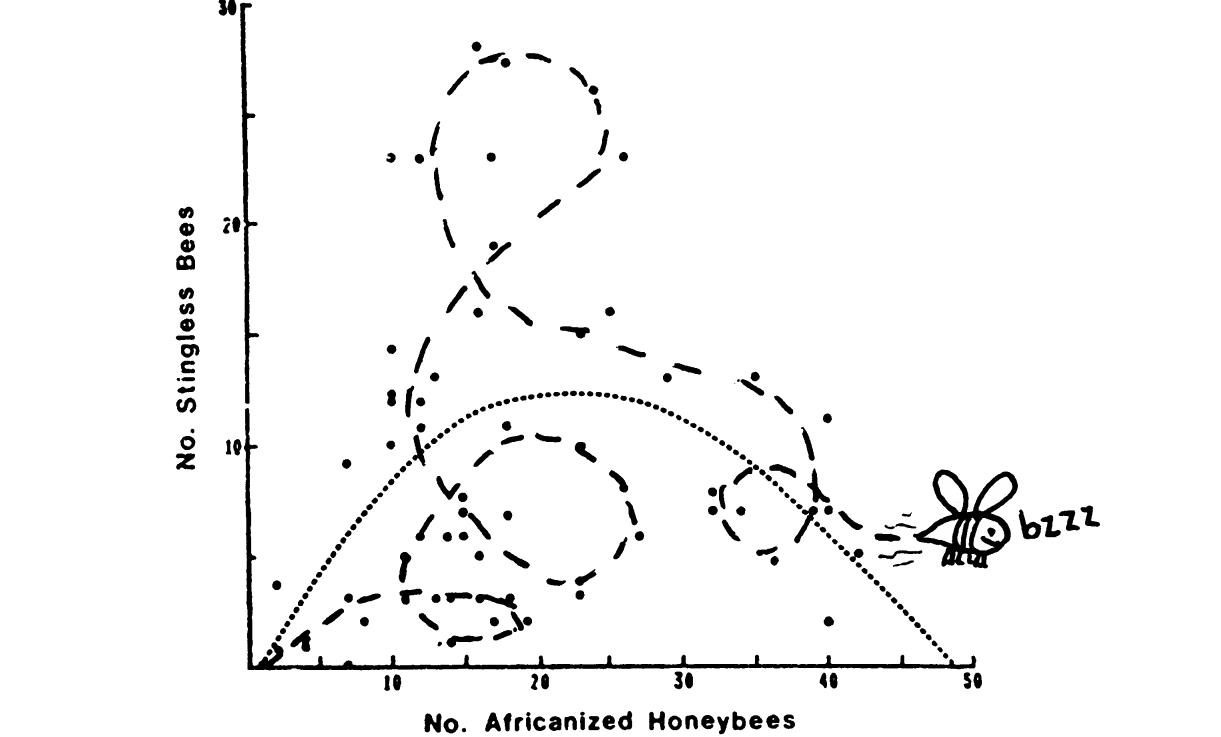
Hazen Robert „Přizpůsobení křivky“. 1978, Science.
- úvod
- Vzorkování zkreslení
- Výběr správného průměru (Dobře zvolený průměr)
- A 10 dalších neúspěšných experimentů, o kterých jsme nepsali
- Hraní si s měřítkem
- Vyberte 100 %
- Skrytí požadovaných čísel
- Vizuální metafora
- Příklad kvalitní vizualizace
- Závěr a další čtení
Vzorkování zkreslení
V roce 1948, během prezidentského klání ve Spojených státech, v noci, kdy byly vyhlášeny výsledky voleb Truman (Demokrati) versus Dewey (Republikáni), zveřejnil Chicago Tribune svůj snad nejslavnější titulek DEWEY PORAŽIL TRUMANA (viz foto) . Noviny ihned po uzavření volebních místností provedly průzkum, obvolaly obrovské množství voličů (dostačující pro vzorek) a vše předznamenalo zvučné vítězství Deweyho. Na fotce vidíme Trumana, vítěze voleb v roce 48, jak se směje. Co se pokazilo?

Lidé byli skutečně voláni náhodně a v dostatečném počtu, ale v roce 48 byl telefon dostupný pouze lidem s určitým příjmem a jen zřídka se nacházel mezi lidmi s nízkými příjmy. Samotný způsob hlasování tedy koriguje rozdělení hlasů. Vzorek nezohlednil dosti širokou vrstvu Trumanových voličů (zpravidla mají demokraté velký podíl na hlasech mezi chudými), pro které byl zase nedostupný telefon. Tento typ vzorkování se nazývá zkreslení vzorkování.
Lidové umění o tomto fenoménu:
Podle online hlasování používá internet 100 % lidí.
Platy absolventů
Překvapilo někoho, že když slyšíme o platech absolventů vysokých škol, z nějakého důvodu jsou tato čísla vždy neuvěřitelně vysoká? V USA se nyní případ dostává dokonce k soudům, kde absolventi tvrdí, že údaje o platech jsou uměle nafouknuté.

(obrázek z Jak lhát se statistikou)
Toto je poměrně starý problém, podle Darrella Huffa měl Yale ’24 podobnou otázku. A ve skutečnosti všichni mluví pravdu, ale ne celou pravdu. Statistiky byly sbírány formou průzkumů (a v těchto letech i papírovou poštou). Odpověď neposílá každý, ale jen malá část všech absolventů; Ti, kterým se daří (což se často odráží v dobrém platu), reagují aktivněji než ostatní, takže vidíme jen tu „dobrou“ část obrázku. To vytváří zkreslení výběru a činí výsledky takových průzkumů zcela nepoužitelnými.
Výběr správného průměru (Dobře zvolený průměr)
Představme si firmu, ve které manažer dostává 25 tisíc, jeho zástupce 7,6 tisíce, vrcholoví manažeři 5,5 tisíce, střední manažeři 3,5 tisíce, junior manažeři 2,5 tisíce a řadoví zaměstnanci 1,4 tisíce (abstraktní libry) měsíčně.
A naším úkolem je prezentovat informace o společnosti v pozitivním světle. Můžeme psát průměrná mzda ve společnosti je X, ale co to znamená průměrný? Zvažme možné možnosti (viz obrázek níže):

(obrázek z Jak lhát se statistikou)
Aritmetický průměr nějaké konečné množiny X=i> je číslo m rovné průměru (X) z rovnice:

To je z pohledu zaměstnance nejužitečnější informace – průměrná mzda je 3,472, ale co odpovídá za tak vysoké číslo? Kvůli vysokým platům vedení, které vytváří iluzi, že zaměstnanec dostane stejnou částku. Z pohledu zaměstnance není tato hodnota nijak zvlášť vypovídající.
Tuto vlastnost „průměrné hodnoty“ v podobě aritmetického průměru samozřejmě neobešlo ani lidové umění.
Úředníci jedí maso, já zelí. Průměrně jíme zelí.
Medián nějakého rozdělení P(X) (X=i>) je hodnota m taková, že splňuje následující rovnici:

Jednoduše řečeno, polovina pracovníků dostává více, než je tato hodnota, a polovina méně – přesně uprostřed distribuce! Tato statistika je pro zaměstnance společnosti poměrně informativní, protože vám umožňuje určit, jak je mzda zaměstnance v porovnání s většinou zaměstnanců.
Mód konečné množiny X=i> je číslo m, které se v X vyskytuje nejčastěji. Móda může být v tomto případě pro člověka, který se chystá začít pracovat v dané firmě, nejinformativnější.
Tedy v závislosti na situaci pod průměrný lze chápat kteroukoli z výše uvedených veličin (v principu a nejen jich). Proto je zásadně důležité pochopit, jak se tato průměrná hodnota počítá.
A 10 dalších neúspěšných experimentů, o kterých jsme nepsali
Do kyseliny sírové dáme obyčejné noviny a do destilované vody časopis TV Park! Cítili jste ten rozdíl? Časopisu se nic nestalo – papír je jako nový! (Celé video je zde.)

Náš výzkum ukazuje, že zubní pasta Doake je o 23 % účinnější než konkurence, a to vše díky zubnímu prášku Dr Cornish’s Tooth Powder! (Který pravděpodobně obsahoval β-karoten a tajný vzorec lesa – pozn. autora.) Možná vás to překvapí, ale ve skutečnosti studii provedli a dokonce vydali technickou zprávu. A experiment skutečně ukázal, že zubní pasta je o 23 % účinnější než její konkurenti (ať už to znamená cokoli). Ale je to celý příběh?
Ve skutečnosti byla velikost vzorku pro experiment pouze tucet lidí (podle Darrella Huffa a již zmíněné knihy). To je přesně ten vzorek, který potřebujete k dosažení jakýchkoli výsledků! Představme si, že si pětkrát hodíme mincí. Jaká je pravděpodobnost, že dostanete hlavy všech pětkrát? (1/2) 5 = 1/32. Je to jen jedna třicet dva, nemůže to být jen náhoda, když se objeví všech pět hlav, ne? Nyní si představte, že tento experiment opakujeme 50krát. Alespoň jeden z těchto pokusů bude úspěšný. Napíšeme o tom ve zprávě, ale všechny další experimenty nikam nevedou. Získáme tak výhradně náhodná data, která dokonale zapadají do našeho úkolu.
Hraní si s měřítkem
Předpokládejme, že zítra musíme na schůzce ukázat, že jsme dohnali naše konkurenty, ale čísla se trochu nesčítají, co bychom měli dělat? Trochu posuneme číselník! Dokonce i New York Times, známé svou kvalitní prací s daty, vytvořily podobný, zcela matoucí graf (všimněte si skoku z 800k na 1,5m ve středu stupnice).

(příklad z How to Display Data Badly od Howarda Wainera. The American Statistician, 1984.)
Vyberte 100 %
Představme si, že loni mléko stálo 10 kopejek za litr a chleba 10 kopejek za bochník. Mléko letos zlevnilo o 5 kop, chleba zdražilo o 20. Pozor, otázka je, co chceme dokázat?

Představme si, že loňský rok je 100%, základ pro výpočty. Mléko pak zlevnilo o 50 % a chleba se zvýšil o 200 %, v průměru o 125 %, což znamená, že celkové ceny vzrostly o 25 %.
Zkusme to znovu, nechť je aktuální rok 100 %, což znamená, že ceny mléka byly loni 200 % a ceny chleba 50 %. To znamená, že v loňském roce byly ceny v průměru o 25 % vyšší!

(grafy a příklad z kapitoly „Jak statistikovat“ Jak lhát se statistikou)
Skrytí požadovaných čísel
Nejlepší způsob, jak něco skrýt, je vytvořit rozptýlení. Zvažte například závislost počtu soukromých a veřejných škol (v tisících) podle roku. Z grafu je patrné, že počet veřejných škol klesá, zatímco počet soukromých se výrazně nemění.
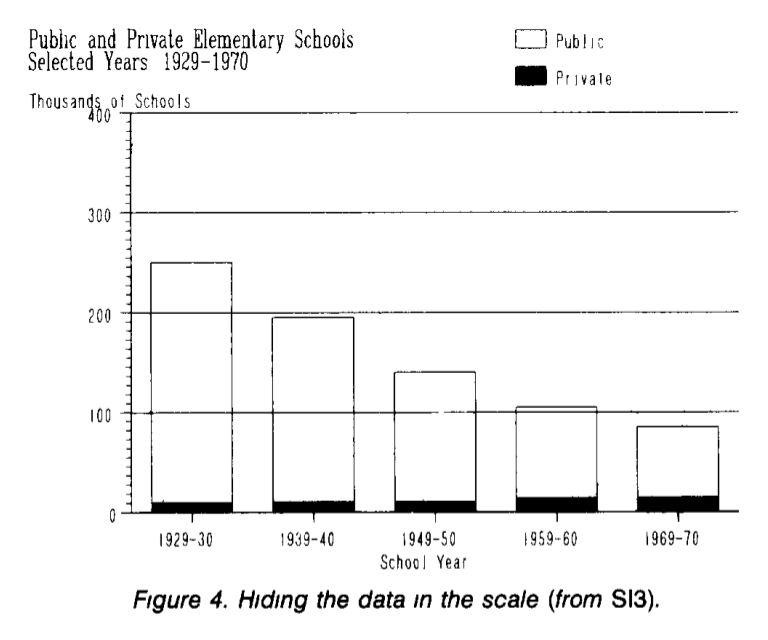
Ve skutečnosti je růst počtu soukromých škol skryt v pozadí počtu škol veřejných. Vzhledem k tomu, že se liší řádově, prakticky žádné změny nebudou na stupnici s dostatečně velkým krokem patrné. Překreslíme počet soukromých škol samostatně; Nyní jasně vidíme výrazný nárůst počtu soukromých škol, který byl „skryt“ v předchozím grafu.
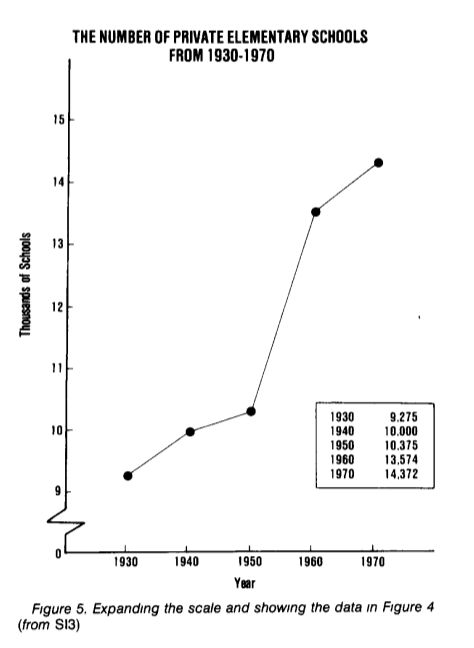
(příklad a grafy z How to Display Data Badly, Howard Wainer. The American Statistician, 1984.)
Vizuální metafora
Pokud nemáte s čím srovnávat, ale opravdu chcete věci zmást, pak je čas na nepochopitelné vizuální metafory. Pokud například vykreslíme do grafu plochu místo délky, jakýkoli růst se bude jevit mnohem větší.
Podívejme se na spotřebu piva v USA v letech 1970-1978 v milionech barelů a podíl společnosti Schlitz na trhu (viz graf níže). Vypadá dobře, působivě. Není to ono?

Nyní se zbavme zbytečných „odpadků“ na tomto grafu a překreslíme jej do normální podoby. Už to nějak nevypadá tak působivě a vážně.

(grafy a příklady od Johna P. Boyda, poznámky k přednášce Jak špatně grafovat aneb co. NEDĚLAT)
První obrázek nelže, všechna čísla na něm jsou správná, ale implicitně prezentuje data ve zcela jiném světle.

(obrázek z Jak lhát se statistikou).
Příklad kvalitní vizualizace
Kvalitní vizualizace především prezentuje výsledky, vyhýbá se nejednoznačnostem a zprostředkovává dostatečné množství informací ve stručném objemu. Dílo Charlese-Josepha Minarda je dobře řečeno zde:
Vše je zde dokonalé, s divákem se nejedná jako s idiotem a neztrácí čas
cenzurováno. Široký béžový pruh ukazuje velikost armády v každém bodě pochodu. V pravém horním rohu je Moskva, kam přichází francouzská armáda a odkud začíná ústup, zobrazená jako černý pruh. Pro větší zajímavost je k ústupové cestě připojen graf času a teploty.
Závěrečný závěr: užaslý divák porovnává velikost armády na startu s tím, co se vrátilo domů. Divák je plný pocitů, naučil se něco nového, cítil měřítko, byl hypnotizovaný, uvědomil si, že se ve škole nic nenaučil.

(Charles Joseph Minard: Napoleonův ústup z Moskvy (Ruské tažení 1812-1813), 1869.)
Závěr a další čtení
76 % všech statistik je převzato z hlavy
Tento výběr zdaleka nepokrývá úplný seznam technik, které vědomě i nevědomě zkreslují data. Tento článek především ukazuje, že musíme velmi pečlivě sledovat statistické údaje, které nám jsou poskytovány, a závěry na jejich základě vyvozované.
Krátký seznam pro další čtení:
Jak lhát se statistikou je nádherná malá knížka, neuvěřitelně zajímavá a dobře napsaná, přečtená jedním dechem. Ukazuje hlavní „chyby“, kterých se média (a nejen ona) při práci s daty dopouštějí.
Jak špatně zobrazovat data. Howard Wainer. The American Statistician (1984) je souborem běžných chyb a obecných „škodlivých“ pravidel, se kterými se nejčastěji setkáváme při práci s vizualizací dat.

- statistika
- špatná rada
- Matematika
