Obsah
5 vědeckých faktů, které vám vrtají hlavou

Lidská logika je opravdu zajímavá věc. Dokáže zmást i sama sebe. To je přesně to, co mnozí myslitelé, filozofové a vědci dělají po více než tisíciletí. Náhodou se tito chlapíci opravdu rádi „baví“ věcmi, které se při použití zmíněné logiky nevejdou do hlavy ani tomu nejneobyčejnějšímu člověku, co se intelektuálních schopností týče.
1. Zenonova dichotomie

Řekové rádi přemýšleli o všem.
Zenón z Eleje, starověký řecký filozof, se pokusil dokázat, že tvrzení o kontinuitě a neomezené dělitelnosti času a prostoru má vážné problémy s logikou.
Tvrdil, že aby člověk zdolal cestu, musí nejprve překonat polovinu cesty. Abyste překonali polovinu, musíte překonat polovinu. A tak dále, do nekonečna. Na základě toho Zeno tvrdil, že pohyb nikdy nezačne (podle tohoto principu).
2. Zenónův šíp

Pokud se nad tím zamyslíte, tak ano.
Další logické veledílo od Zeno, s jehož pomocí se snažil porozumět pohybu. Navzdory paradoxnosti výroku právě díky němu začala ve vědě diskuse o povaze času. Ještě není hotovo. A celé to znělo nějak takto:
Letící šíp je nehybný, protože v každém okamžiku zaujímá stejnou pozici nebo jinými slovy je v klidu. A protože je v každém okamžiku v klidu, je v klidu ve všech chvílích času, jinak neexistuje žádný okamžik v čase, kdy by udělal pohyb.
3. Theseova loď

Všechno je pro Theseuse velmi špatné.
Paradox je velmi jednoduchý. Zní to takto:
Pokud byly vyměněny všechny součásti objektu, je objekt stále stejným objektem?
Tento paradox popsal Plutarchos, starověký řecký spisovatel a filozof. Vycházel z úvah o lodi Theseus, na které se vracel z Kréty do Athén. Loď byla držena několik set let a byla každý rok posílána s velvyslanectvím do Delosu. Rok co rok se při opravách vyměňovala prkna v lodi, což vedlo filozofy k tomuto způsobu myšlení.
4. Paradox všemohoucnosti

Co když Bůh, a ne Bůh.
Tento paradox je jednoduchý a filozofové s jeho pomocí rádi dokazují, že žádný bůh nemůže existovat. A zní to jako otázka: „Bude všemocná bytost schopna vytvořit kámen, který nemůže zvednout?“ Odpověď „ano“ i odpověď „ne“ vedou k tomu, že taková bytost nebude všemocná.
5. Malířův paradox

Prostě bez fantazie.
Paradox zní jednoduše: postava s nekonečnou plochou může být natřena konečným množstvím barvy.
Abyste pochopili, musíte si představit nekonečnou stupňovitou desku. Ať se skládá z obdélníků. První z nich je čtverec o straně 1 cm Každý další je dvakrát užší a dvakrát delší než ten předchozí. Výsledkem je nekonečná plocha desky. Pokud figuru otočíte kolem její rovné hrany, stane se trojrozměrnou a bude se skládat z válců. Pokud to spočítáte, jeho objem se rovná 2*Pi cm3, což znamená, že jej lze naplnit konečným množstvím barvy ponořením nekonečné desky do nádoby.
6. Grelling-Nelsonův paradox

Dobrá otázka pro učitele jazyků.
Představme si, že se v jazyce objevila přídavná jména autologická a heterologická. Nyní všechna přídavná jména spadají do těchto dvou tříd. Autologické přitom popisují pouze sebe, zatímco heterologické pouze jiné lidi.
Otázka paradoxu zní takto: do jaké kategorie by tedy mělo být slovo „heterologní“ zařazeno? Pokud se tedy jedná o autologické přídavné jméno, pak musí mít označenou vlastnost a v tomto případě se stane heterologickým. Pokud je však dané přídavné jméno heterologické, pak by nemělo mít jméno, což znamená, že nemůže být tím, čím je.
7. Úlovek-22

Dokonce o ní napsali knihu a natočili film.
Člověk, který je nepříčetný, může požádat o osvobození od vojenské povinnosti. Avšak každý, kdo se na požádání pokusí vyhnout bojové povinnosti, není skutečně blázen.
8. Paradox zajímavých čísel

Je to legrační, že?
„Jednička“ je první nenulové přirozené číslo. „Dva“ je nejmenší prvočíslo. „Tři“ je první liché prvočíslo. „Čtyři“ je nejmenší složené číslo. Pokud budeme pokračovat v myšlence a rozdělíme všechna přirozená čísla na „zajímavá“ a „nezajímavá“, ukáže se, že všechna přirozená čísla jsou zajímavá.
Pokud totiž v matematice existuje neprázdná množina nezajímavých přirozených čísel, pak bude obsahovat nejmenší číslo. Zajímavé je nejméně nezajímavé číslo, což znamená, že v tom všem je rozpor.
9. Paradox opilce

Obor formální logiky. Tento paradox říká, že v každém baru je alespoň jeden člověk, pro kterého platí, že když pije, tak pijí všichni. Nyní řekněme, že všichni v baru pijí. Pro každého pak platí výše popsané tvrzení, že když pije, tak pijí všichni. Pokud to není pravda, pak je v baru alespoň jeden člověk, který nepije. A tak, protože je nyní falešné, že pije, je pravda, že když pije, pijí všichni.
10. Paradox přátelství
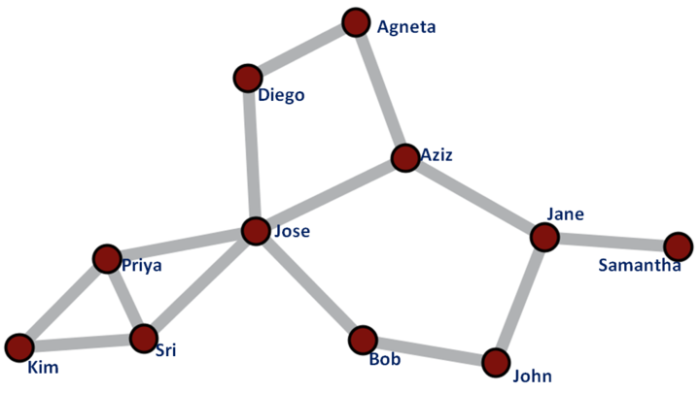
Teď už se nemusíte bát.
Tento paradox naznačuje, že většina lidí má méně přátel, než je průměr jejich přátel. Ačkoli toto tvrzení zní paradoxně, bylo matematicky podloženo. Logické vysvětlení je odvozeno ze základních principů teorie grafů. To bylo potvrzeno v roce 2012.
