Obsah
- 1 6 způsobů, jak najít oblast lichoběžníku
- 2 Plocha lichoběžníkového online kalkulátoru (5 způsobů)
- 3 Plocha lichoběžníku
- 4 Jaká je plocha lichoběžníku
- 5 Užitečné informace o oblasti lichoběžníku
- 6 Vzorce pro lichoběžníkové plochy
- 7 Přes základny a výšky
- 8 Přes úhlopříčky a úhel mezi nimi
- 9 Přes čtyři směry
- 10 Problémy při hledání oblasti lichoběžníku s řešeními
- 11 1 výzva
- 12 2 výzva
- 13 Oblíbené otázky a odpovědi
- 14 Jak se měří plocha lichoběžníku?
- 15 Proč potřebujete umět vypočítat plochu lichoběžníku v 8. třídě?
- 16 Proč byste v životě mohli potřebovat schopnost najít oblast lichoběžníku?
6 způsobů, jak najít oblast lichoběžníku
Plocha lichoběžníkového online kalkulátoru (5 způsobů)
toto online kalkulačka trapézové plochy pomoci najít oblast lichoběžníku. Řešení lze nalézt pomocí pěti různých metod.
Pomocí této kalkulačky můžete získat podrobné řešení krok za krokem s vysvětlením a odvozením vzorců. Díky tomu budete schopni porozumět algoritmus pro nalezení oblasti lichoběžníku.
- Kalkulačka
- Návod
- Teorie
- Příběh
- Nahlásit problém
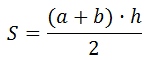
Lichoběžník je čtyřúhelník, ve kterém jsou dvě strany rovnoběžné (základny) a další dvě rovnoběžné (strany).
Vzorec pro oblast lichoběžníku, kde aab jsou základny, h je výška
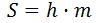
Lichoběžník je čtyřúhelník, ve kterém jsou dvě strany rovnoběžné (základny) a další dvě rovnoběžné (strany).
Vzorec pro oblast lichoběžníku, kde m je středová čára, h je výška
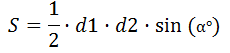
Lichoběžník je čtyřúhelník, ve kterém jsou dvě strany rovnoběžné (základny) a další dvě rovnoběžné (strany).
Vzorec pro oblast lichoběžníku, kde d1,d2 jsou úhlopříčky, α° je úhel mezi nimi
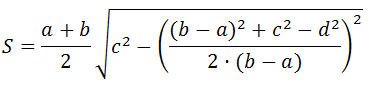
Lichoběžník je čtyřúhelník, ve kterém jsou dvě strany rovnoběžné (základny) a další dvě rovnoběžné (strany).
Vzorec pro oblast lichoběžníku, kde aab jsou základny, c a d jsou strany
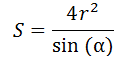
Lichoběžník je čtyřúhelník, ve kterém jsou dvě strany rovnoběžné (základny) a další dvě rovnoběžné (strany).
Vzorec pro oblast lichoběžníku, kde r je poloměr vepsané kružnice, α° je úhel mezi základnou a stranou
- Vyberte způsob hledání oblasti. Výběr metody závisí na datech, která máte.
- Zadejte informace o trapéz v příslušném poli.
- Klikněte na tlačítko „Vypočítat“ a na obrazovce se objeví výsledek s řešením krok za krokem.
Posledních 20 výpočtů na této kalkulačce
- Plocha lichoběžníku se základnami 1210,350 a výškou 300 je 234000
- Plocha lichoběžníku se stranami 4,8.49,3.358,3.358 je 15.59
- Plocha lichoběžníku se základnami 4.22,2.43 a výškou 2.5 je 8.313
- Plocha lichoběžníku se středovou osou 8 a výškou 11 je 88
- Plocha lichoběžníku se základnami 260,208 a výškou 52 je 12168
- Plocha lichoběžníku se základnami 6,10 a výškou 32 je 256
- Plocha lichoběžníku se stranami 8,4,6,7 je 35.93
- Plocha lichoběžníku se základnami 17.7,3.65 a výškou 7.65 je 81.66
- Plocha lichoběžníku se základnami 13,5 a výškou 5 je 45
- Plocha lichoběžníku se základnami 17.7,3.65 a výškou 7.56 je 80.7
- Plocha lichoběžníku se základnami 3.65,17.7 a výškou 7.65 je 81.66
- Plocha lichoběžníku se stranami 3.132,3.132,1.486,1.519 je 4.654
- Plocha lichoběžníku se stranami 1.486,1.519,3.132,3.16 je 2.502
- Plocha lichoběžníku se stranami 1.486,1.519,3.132,3.15 je 3.955
- Plocha lichoběžníku se stranami 1.486,1.519,3.132,3.14 je 4.571
- Plocha lichoběžníku se stranami 1.486,1.519,3.132,3.132 je 4.706
- Plocha lichoběžníku se základnami 3.65,5.5 a výškou 7.4 je 33.86
- Plocha lichoběžníku se stranami 5.2,0.9,6.5,4.55 je 13.83
- Plocha lichoběžníku se stranami 1.49,1.52,3.13,3.14 je 4.449
- Plocha lichoběžníku se stranami 19,20,3.4,1.5 se rovná NAN
Pokud máte s touto kalkulačkou nějaké problémy, dejte nám prosím vědět.
Po výpočtu klikněte na tlačítko „Výpočet je nesprávný“, pokud najdete chybu. Nebo klikněte na „Výpočet je správný“, pokud nejsou žádné chyby.
Nejprve proveďte výpočet na této kalkulačce. Tak sem zase přijď.
Trapezium je čtyřúhelník, ve kterém jsou dvě strany rovnoběžné (základna) a další dvě rovnoběžné (strany).
Plocha lichoběžníkuje číselná charakteristika charakterizující velikost roviny ohraničené geometrickým obrazcem tvořeným čtyřmi za sebou spojenými segmenty (stranami), ve kterých jsou dvě protilehlé strany po párech rovnoběžné (základy lichoběžníku) a další dvě rovnoběžné (tzv. strany strapezia).
Plocha lichoběžníku
Od architektury po finance, od geografie po výrobu, znalost tohoto vzorce může být užitečná pro každého. Naučte se používat oblast lichoběžníku k řešení různých problémů a optimalizaci vaší práce

Plocha lichoběžníku není jen matematický koncept, ale univerzální nástroj pro výpočet plochy v různých oblastech činnosti.
Jaká je plocha lichoběžníku
Lichoběžník je konvexní čtyřúhelník, ve kterém jsou dvě strany rovnoběžné a další dvě rovnoběžné.
Rovnoběžné strany a; b – základny, nikoli rovnoběžné strany c; d – boční („nohy“).
h – výška, vzdálenost mezi rovnoběžnými stranami (kolmá délka).

Plocha lichoběžníku je část roviny obsažená v daném obrazci. Plochu lichoběžníku lze určit počtem jednotkových čtverců, které se do něj vejdou.
Například lichoběžník obsahuje 14 jednotkových čtverců o straně 1 cm – což znamená, že jeho plocha je 14 cm2.
Užitečné informace o oblasti lichoběžníku
| Kdo jako první našel oblast lichoběžníku? | Ve starověkém Řecku dokázali Pythagoras a Euclid najít oblast lichoběžníku v Egyptě, vzorec byl použit při stavbě pyramid. V dílech arabských matematiků Al-Khorezmiho a Al-Karafiho byly navrženy metody pro jeho nalezení, ale kdo byl první, není známo. |
| Jak najít oblast lichoběžníku, pokud je známa délka jeho střední čáry | Středová čára lichoběžníku je segment spojující středy stran. Je rovnoběžná se základnami a rovná se jejich polovičnímu součtu.m = (a+b): 2 S = m ∙ h |
| Pokud se polygon skládá z několika polygonů, pak je jeho plocha rovna součtu ploch těchto polygonů | Tato vlastnost oblastí platí také pro lichoběžník, protože jej lze rozdělit na různé mnohoúhelníky, jako jsou dva trojúhelníky a obdélník. |
Vzorce pro lichoběžníkové plochy
Není vždy možné vypočítat plochu lichoběžníku nakreslením jednotkových čtverců. V tomto případě je jednodušší použít vzorce.
Přes základny a výšky

Plocha lichoběžníku se rovná součinu poloviny součtu délek základen a délky jeho výšky.
(mathrm S;=;frac 2;;cdot;mathrm h)
Tento vzorec se nejčastěji používá při řešení problémů.
Přes úhlopříčky a úhel mezi nimi
Pokud jsou známy hodnoty úhlopříček lichoběžníku a úhel mezi nimi, můžete pro výpočet plochy lichoběžníku použít následující vzorec:
S = 0,5 ∙ d1 ∙ d2 ∙ hřích α =
= 0,5 ∙ d1 ∙ d2 ∙ hřích β

Přes čtyři směry

Pokud je strana a větší než strana b (a > b), strana c je větší než strana d (c > d), můžete použít vzorec:
Problémy při hledání oblasti lichoběžníku s řešeními
Uveďme své znalosti do praxe.
1 výzva
Lichoběžník je vyobrazen na kostkovaném papíře o velikosti čtverce 11. Najděte jeho oblast. Při pohledu na lichoběžník je vidět, že má pro nás neobvyklý tvar. Jedná se o lichoběžník se dvěma protilehlými úhly, které jsou tupé.

Problém lze vyřešit dvěma způsoby. Podívejme se na obojí. První metoda: podle vzorce.
Vzhledem k: trapeze
a = 12 jednotek
b = 8 jednotek
h = 6 jednotek
Hledat: S
řešení:
(mathrm S;=;frac 2;;cdot;mathrm h)
Dosazujeme a počítáme.
Druhá cesta

Lichoběžník rozdělíme na části: dva trojúhelníky a čtverec.
Trojúhelníky dokončíme tak, aby vznikl obdélník. Spočítáme počet buněk v každé a rozdělíme na polovinu.
Máme 6 čtverečních jednotek a 18 čtverečních jednotek. Počítáme buňky do čtverce, je jich 36 čtverečních jednotek.
Nyní pomocí vlastnosti oblastí najdeme součet oblastí našich částí:
S = 6 + 18 + 36 = 60 čtverečních. Jednotky
Odpověď: 60 čtverečních jednotek.
2 výzva

Najděte plochu lichoběžníku, pokud jsou délky úhlopříček 12 cm a 8 cm a úhel mezi nimi je 60 0.
Vzhledem k: trapeze
Hledat: S
řešení: S = 0,5 ∙ d1 ∙ d2 ∙ hřích α
Dosazujeme a počítáme.
S = 0,5 ∙12 ∙ 8 ∙ hřích 60 0 = 1 /2 ∙ 12 ∙ 8 ∙ √3 /2 = 24√3 cm 2
Odpověď: 24√3 cm 2
Oblíbené otázky a odpovědi
Jak se měří plocha lichoběžníku?
Plocha lichoběžníku se měří ve čtvercových jednotkách, to znamená v mm 2, cm 2, dm 2, m 2 a tak dále.
Proč potřebujete umět vypočítat plochu lichoběžníku v 8. třídě?
Již od základní školy se děti seznamují se čtyřúhelníky: obdélník a čtverec v 8. třídě, jejich znalostní základna se zvyšuje díky novým dovednostem a schopnostem (stupně, aritmetické odmocniny atd.), tak je tomu i v této třídě; že kapitoly „Čtyřúhelníky“ a „Oblasti čtyřúhelníků“.
V závěrečných testech OGE a Jednotné státní zkoušky je mnoho úloh s lichoběžníkem, jak s krátkým řešením, tak s podrobným, proto se seznamujeme s různými typy úloh a řešíme je již od 8. třídy.
Proč byste v životě mohli potřebovat schopnost najít oblast lichoběžníku?
Lichoběžník a jeho oblast jsou široce používány v životě. Například ve stavebnictví často najdete střechy domů se dvěma stranami ve tvaru lichoběžníku, což znamená, že musíte vypočítat plochu, abyste mohli zakoupit požadované množství materiálu.
Pro návrháře při tvorbě dámských tašek a oblečení.
V ekonomice, zemědělství a dalších oblastech. No, ve škole – za úspěšné složení zkoušek.
