8 způsobů, jak zjistit obvod kruhu

Kružnice (kruh) je geometrický útvar v rovině, jehož všechny body jsou stejně vzdálené od daného bodu (středu kružnice).
Vzorec pro obvod: kde R je poloměr kruhu.

Kružnice (kruh) je geometrický útvar v rovině, jehož všechny body jsou stejně vzdálené od daného bodu (středu kružnice).
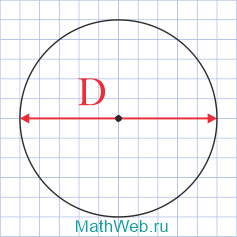
Vzorec pro obvod: kde D je průměr kruhu.

Kružnice (kruh) je geometrický útvar v rovině, jehož všechny body jsou stejně vzdálené od daného bodu (středu kružnice).
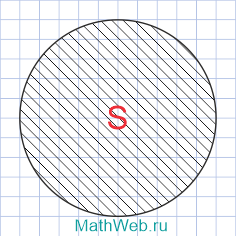
Vzorec pro obvod: kde S je plocha kruhu.

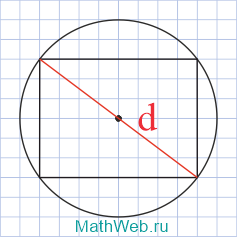
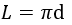
Kružnice (kruh) je geometrický útvar v rovině, jehož všechny body jsou stejně vzdálené od daného bodu (středu kružnice).
Vzorec pro obvod: kde d je úhlopříčka vepsaného obdélníku.

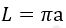
Kružnice (kruh) je geometrický útvar v rovině, jehož všechny body jsou stejně vzdálené od daného bodu (středu kružnice).
Vzorec pro obvod: kde a je strana opsaného čtverce.

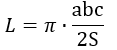
Kružnice (kruh) je geometrický útvar v rovině, jehož všechny body jsou stejně vzdálené od daného bodu (středu kružnice).
Vzorec pro obvod: kde a, b, c jsou strany opsaného trojúhelníku, S je jeho obsah.

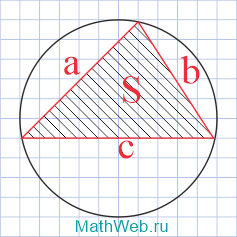
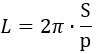
Kružnice (kruh) je geometrický útvar v rovině, jehož všechny body jsou stejně vzdálené od daného bodu (středu kružnice).
Vzorec pro obvod: kde p je půlobvod vepsaného trojúhelníku, S je jeho obsah.

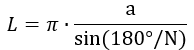
Kružnice (kruh) je geometrický útvar v rovině, jehož všechny body jsou stejně vzdálené od daného bodu (středu kružnice).
Vzorec pro obvod kruhu: kde a je strana vepsaného mnohostěnu, N je počet stran.

1. Vyberte metodu pro zjištění obvodu kruhu. Volba závisí na počátečních datech na kruhu.
2. Do příslušných polí zadejte údaje o obvodu.
3. Klikněte na tlačítko „Vypočítat“ a výsledek se objeví na obrazovce.

Posledních 20 výpočtů na této kalkulačce

1. Délka kružnice o poloměru R = 55 je 345.57
2. Délka kruhu o průměru D = 1700 je 5340.6
3. Délka kružnice s vepsaným pravidelným mnohostěnem se stranou a = 5 a počtem stran N = 4 je 22.21
4. Délka kružnice o poloměru R = 710 je 4460.9
5. Obvod kruhu o ploše S = 8 je 3.166
6. Délka kruhu o průměru D = 4.75 je 14.92
7. Délka kruhu o průměru D = 4.5 je 14.14
8. Délka kružnice o poloměru R = 325 je 2042
9. Obvod kruhu se čtvercem opsaným stranou a = 672 je 2111.1
10. Obvod kruhu se čtvercem opsaným stranou a = 10 je 31.42
11. Délka kruhu o průměru D = 0.057 je 0.1791
12. Délka kruhu o průměru D = 0.05 je 0.1571
13. Délka kružnice s vepsaným pravidelným mnohostěnem se stranou a = 9 a počtem stran N = 3 je 32.64
14. Délka kružnice s vepsaným pravidelným mnohostěnem se stranou a = 15 a počtem stran N = 13 je 196.85
15. Délka kruhu o průměru D = 225 je 706.84
16. Délka kružnice s vepsaným pravidelným mnohostěnem se stranou a = 5.3 a počtem stran N = 3 je 19.23
17. Délka kruhu o průměru D = 138 je 433.53
18. Obvod kruhu o ploše S = 15 je 3.705
19. Obvod kruhu o ploše S = 800 je 10.01
20. Délka kružnice o poloměru R = 400 je 2513.2

Pokud máte s touto kalkulačkou nějaké problémy, dejte nám prosím vědět.

Po výpočtu klikněte na tlačítko „Výpočet je nesprávný“, pokud najdete chybu. Nebo klikněte na „Výpočet je správný“, pokud nejsou žádné chyby.

Nejprve proveďte výpočet na této kalkulačce. Tak sem zase přijď.

Obvod nebo obvod kruhu je délka křivky složené z mnoha bodů, které kruh obklopují.
Obvod kruhu lze nalézt podle délky dráhy, kterou kruh potřebuje k dokončení jedné celé otáčky.

Jak zjistit obvod kruhu?

Zjištění obvodu je velmi snadné pomocí naší online kalkulačky. Délku lze také zjistit nezávisle pomocí vzorců. Výběr požadovaného vzorce závisí na tom, jaké údaje jsou známy.

1) Poloměr

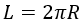
kde R je poloměr kružnice.

2) Podle průměru

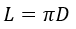
kde D je průměr kruhu.

3) Podle oblasti kruhu

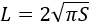
kde S je plocha kruhu.

4) Diagonálně vepsaný obdélník

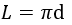
kde d je úhlopříčka vepsaného obdélníku.

5) Po straně popsaného čtverce

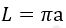
kde a je strana opsaného čtverce.

6) Podle stran a plochy opsaného trojúhelníku

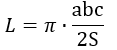
kde a, b, c jsou strany opsaného trojúhelníku, S je jeho obsah.

7) Podle oblasti vepsaného trojúhelníku

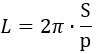
kde p je půlobvod vepsaného trojúhelníku, S je jeho obsah.

8) Po straně vepsaného mnohostěnu

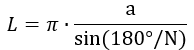
kde a je strana vepsaného mnohostěnu, N je počet stran.

Obvod

Pro jakýkoli geometrický obrazec můžete najít obvod – celkovou délku hranic obrazce. Například pro čtverec, obdélník nebo trojúhelník je třeba sečíst délky všech stran. Jak vypočítat obvod kruhu, pokud nemá žádné strany? To lze provést pomocí různých vzorců a na základě původně známých dat.

Co je obvod

Obvod je celková délka okraje kruhu. V matematice se obvod kruhu označuje latinskými písmeny C nebo L. V tomto článku budeme používat první.

Užitečné informace o obvodu

Obvod – záhada z dávných dob	Od starověku byli vědci schopni určit obvod, ale s určitou mírou chyby. Ve 3. století př. Kr. Starověký řecký vědec Archimedes ze Syrakus odvodil vzorec, který používáme dodnes.
Bez čísla π se neobejde	Všechny vzorce pro výpočet obvodu kruhu obsahují jednu z nejdůležitějších matematických konstant – číslo π, rovné přibližně 3,14
Pro označení obvodu kruhu jsou dvě možnosti	Obvod se značí písmeny C a L. Nejčastěji se používá první možnost.

Vzorce pro obvod

Obvod kruhu lze vypočítat různými způsoby na základě toho, jaká data máme.

Přes průměr kruhu

Známe-li průměr kruhu, pak lze obvod vypočítat vynásobením čísla π průměrem. Průměr kružnice je úsečka spojující dva body na kružnici, procházející středem kružnice.

Přes poloměr kruhu

Známe-li poloměr kružnice, je obvod součinem 2π a poloměru. Připomeňme, že poloměr je segment od středu kruhu k libovolnému bodu na něm. Průměr se rovná dvěma poloměrům.

Přes oblast kruhu

Pokud známe plochu kruhu, pak nalezení obvodu vyžaduje složitější výpočty.

Připomeňme si tedy vzorec pro výpočet plochy kruhu:

Z tohoto vzorce můžeme vypočítat poloměr kružnice, který se rovná poloměru kružnice, se kterou určíme obvod.

Po zjištění poloměru kruhu vypočítáme obvod pomocí vzorce:

(mathrm C;=;2mathrmpi;cdot;mathrm r)

Úlohy při hledání obvodu kruhu s řešením

Následující úlohy vám pomohou procvičit si výpočet obvodu kruhu pomocí různých vzorců.

1 výzva

Poloměr kruhu je 3 cm.

Vzhledem k:

Hledat: С

řešení: protože známe poloměr a hodnotu čísla π, lze obvod vypočítat pomocí vzorce C = 2π ∙ r

C = 2 ∙ 3,14 ∙ 3

Odpověď: obvod je 18,84 cm.

2 výzva

Průměr kruhu je 8 dm. Určete obvod.

Vzhledem k:

Hledat: С

řešení: v tomto problému známe průměr kruhu, takže pro výpočet obvodu můžeme použít vzorec

C = π ∙ d

C = 3,14 ∙ 8

Odpověď: obvod je 25,12 dm

to je zajímavé
Oblast kruhu
Vzorce a neobvyklé způsoby výpočtu plochy kruhu

3 výzva

Je známo, že plocha kruhu je 25 m.

Vzhledem k:

Hledat: С

řešení:

1) vypočítejte poloměr kružnice pomocí vzorce r = √ s /_π

r = √ 25 /_3,14

2) zjistěte obvod přes poloměr pomocí vzorce C = 2π ∙ r

C = 2 ∙ 3,14 ∙ 2,82

Odpověď: obvod je 17,7m.

Oblíbené otázky a odpovědi

Odpovídá Ljudmila Samoroková, učitelka matematiky, odbornice na přípravu na Jednotnou státní zkoušku a Jednotnou státní zkoušku z matematiky

Jak jednoduchými slovy vysvětlit, jaký je obvod kruhu?

Obvod je délka uzavřené přímky, která kruh uzavírá.

Pokud umístíte bod a kolem něj ve stejné vzdálenosti nakreslíte velké množství bodů a spojíte je do jedné uzavřené čáry, dostanete kruh. A původně umístěný bod se stane středem kruhu.

Jak se měří obvod?

Obvod kruhu má jednotky měření, jako každá délka – metr, decimetr, centimetr, milimetr, kilometr.

Proč potřebujete v 6. třídě umět vypočítat obvod kruhu?

Učíme děti uplatňovat znalosti, které získají ve škole, v životě. Jak měřit obvod v životě? Stačí vzít nit a změřit obrys kruhu. Tato měření ale nikdy nebudou přesná. Co když není po ruce žádná nit? Co když je kruh tak velký, že tam není dostatek nití? Do 6. třídy mají děti dostatečné matematické porozumění a potřebné dovednosti k nalezení neznámé veličiny prostřednictvím známé. Navíc se děti v 6. třídě seznamují s desetinnými zlomky a učí se je zaokrouhlovat. Když se ale podíváme do článku, uvidíme, že výpočet obvodu kruhu se neobejde bez nejznámějšího desetinného zlomku – konstanty, čísla π. Matematické dovednosti navíc umožňují dětem na základě podmínek problému (pochopení známé veličiny) zvolit způsob výpočtu, který lze v daném případě aplikovat.