Obsah
5 úloh z matematické olympiády, které nezvládne každý dospělý
Úkoly 1. kola XV olympiády v matematice pro 5. ročník

Udělejte si zkušební matematickou olympiádu pro ročníky 1–9.
PASS ZDARMA
1. kolo XV. matematické olympiády se konalo od 15. ledna do 6. února 2024
Cíle olympiády
Úloha №1
Mezi žáky 4. třídy „M“ byli všichni buď na exkurzi, nebo v divadle nebo na vandru. Všichni, kdo byli v divadle, šli po představení na prohlídku. Lidí, kteří nebyli na túře, je méně než těch, kteří na exkurzi nebyli. Na které akci bylo nejvíce dětí?
(A) na exkurzi (B) v divadle (C) na túře (D) nelze určit
Úloha №2
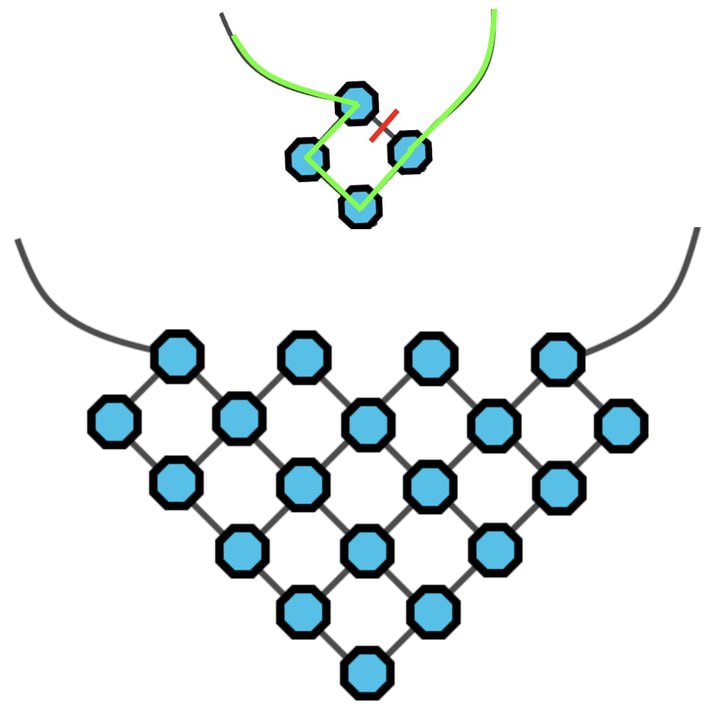
Kolik nití mezi diamanty se musí ustřihnout, aby se velký diamantový náhrdelník na obrázku změnil v diamantovou nit, pokud mají být na nit navlečeny všechny korálky z náhrdelníku? Například u náhrdelníku se čtyřmi korálky byste museli ustřihnout pouze jeden pramen, jak je znázorněno níže.
(A) 8 (B) 9 (C) 10 (D) 11 (E) 12
Aby na profesora Tinyho Tsakhes udělal dojem, přidal osm čísel v řadě a výsledek napsal na tabuli. Profesor však řekl, že ve výpočtech došlo k chybě. Ukázalo se, že se Little Tsakhes mýlil doslova o jednu. Jaké číslo lze napsat na tabuli?
(A) 52 (B) 44 (C) 123 (D) 156
Úloha №4
Vasya našel nejmenší přirozené číslo, jehož součin číslic je roven 72, a odečetl od něj součet jeho číslic. Jakého výsledku dosáhl?
(A) 72 (B) 81 (C) 234 (D) 252 (E) mezi výše uvedenými neexistuje žádná správná odpověď
Úloha №5
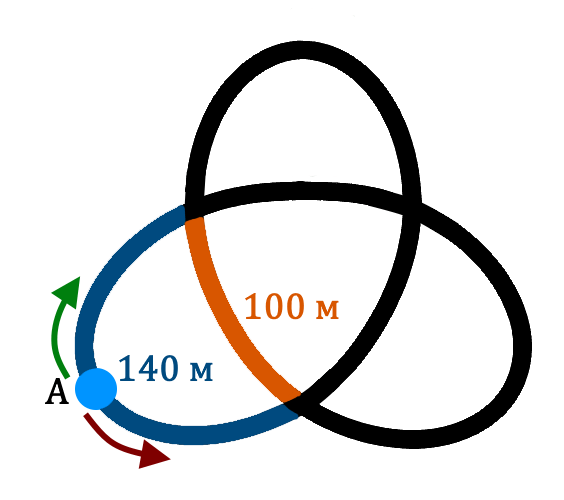
Ve městě N byl postaven neobvyklý běžecký pás. Dva atleti startují současně z bodu A (uprostřed modré trati), běží v opačných směrech stejnou rychlostí. Na rozcestí se mohou otočit kdekoli, ale ne v opačném směru. Každý sportovec uběhl 2 kilometry. Kolikrát se maximálně mohli potkat, nepočítám-li setkání na startu, pokud během celého tréninku ani jednou neběželi vedle sebe?
(A) 16 (B) 15 (C) 17 (D) 6 (E) 7
Na úsečce AD o délce 33 centimetrů jsou body B a C tak, že: body jsou uspořádány v pořadí ABCD; segment BC je dvakrát delší než segment AB; a segment CD je 4krát delší než BC. Najděte délku segmentu AC
(A) 8 (B) 9 (C) 12 (D) 18
Úloha №7
15 čokolád je těžších než 19 karamelů, ale 3 čokolády jsou lehčí než 4 karamelky. Když bylo na jednu pánev váhy umístěno 9 karamelů a na druhou několik čokolád, váhy byly v rovnováze. Kolik čokolád jste dali na váhu?
(A) 5 (B) 6 (C) 7 (D) 8
Úloha №8
Malá opice sní všechno ovoce ze stromu za 6 hodin a její matka a otec (každý zvlášť) je sní dvakrát rychleji. Jak dlouho bude trvat, než rodina opic sní všechny plody ze stromu společně?
