Britský televizní moderátor hovořil o neobvyklém „ruském“ způsobu násobení čísel

Britský matematik obdivoval „ruskou metodu násobení“ ze starověkého Egypta

7. února – EgyptHome.org. Britský popularizátor matematiky Johnny Ball hovořil na kanálu YouTube Numberphile o Ruština, nebo spíše starověký egyptský metoda násobení. Vědec se stal hostem projektu, o kterém píše portál PolitRussia.

Když ho tato informace zasáhla, podělil se o své vzpomínky z dětství. Už jako malý chodil s rodiči po hospodách Bristol, kde byly za druhé světové války speciální pokoje pro potomky, které tam rodiče nechali a chodili na denní směny do továrny.

Na jednom z těchto míst se Ball setkal s mladým mužem, který mu řekl o „úžasné metodě násobení“ Rusů, jejíž podstata se scvrkává na metodu interakce polovin a zdvojnásobení čísel.

„Rusové nepoužívají věci, které se jim nelíbí. Jedna z věcí, které nemají rádi, jsou zlomky,“ poznamenal Ball.

Podstatou metody je použití půlek a zdvojení. Aby bylo možné v takovém systému vynásobit dvě čísla – bez ohledu na počet číslic a třídu – je nutné uspořádat násobitel a násobitel ve formě dvou sloupců – levého a pravého. Každý řádek levého sloupce bude obsahovat čísla rovnající se polovině výše uvedeného, ​​ale bez zlomků. To znamená, že nemluvíme o zaokrouhlování, ale o pouhém přeškrtnutí. Například vynásobením 9 13 ve druhém řádku levého sloupce po dělení 9 2 by mělo být 4,5, ale podle britského matematika musí být zlomek 0,5 vynechán.

V pravém sloupci se každé nižší číslo zdvojnásobí a takto to bude pokračovat, dokud se číslo v levém sloupci metodou půlek nezmění v jedničku. Pokud budeme pokračovat v příkladu násobení 9 x 13, měla by být v pravém sloupci (shora dolů) uvedena následující čísla: 13, 26, 52, 104.

Poté jsou všechny řádky, kde jsou v levém sloupci vyznačena sudá čísla, zcela přeškrtnuty. To znamená, že v případě vynásobení 9 13 zbude pouze první a poslední řádek. A teprve potom se sečtou všechna zbývající čísla z pravého sloupce – to bude požadované číslo (13+104=117).

Dodejme jen, že se počítá z tzv. „ruské metody“. starověký Egypt.

V Británii si vzpomněli na „ruskou rolnickou metodu množení“

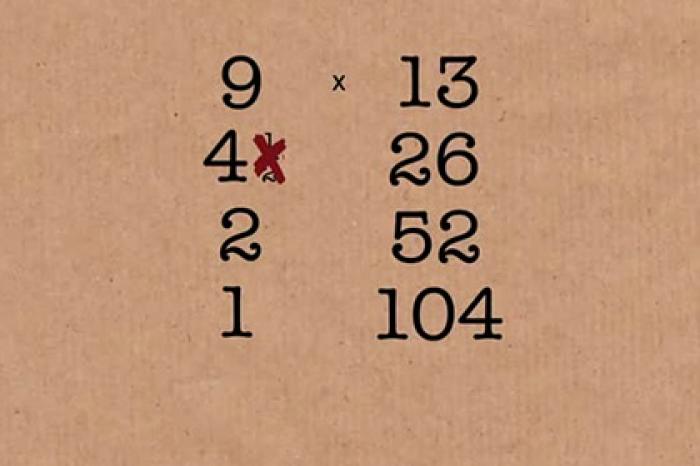
Britský televizní moderátor a popularizátor matematiky Johnny Ball v další epizodě Numberphile dostupné na YouTube připomněl ruskou rolnickou metodu násobení.

Jako příklad jsme uvažovali vynásobení 9 13. Výpočet byl proveden ve dvou sloupcích. Vlevo – 9 bylo děleno 2, vpravo – 13 bylo násobeno 2. Výsledky (minus zlomková část v prvním případě) byly zapsány pod původní čísla. Poté se postup opakuje (4 se dělí 2 a 26 se násobí 2). Výsledkem jsou dva sloupce (9, 4, 2, 1 a 13, 26, 52, 104). Poté musíte přeškrtnout řádky, kde jsou vlevo sudá čísla (4 a 26, 2 a 52). Sečtením zbývajících čísel vpravo (13, 104) by se měla dostat požadovaná odpověď (117).

Ball zdůrazňuje, že ruští rolníci používali tuto metodu v 19. století, ale byla známa již ve starověkém Egyptě, přímo sahající k binárnímu číselnému systému.

V srpnu 2015 bylo oznámeno, že matematici z Washingtonské univerzity v Bothellu objevili nový typ pětiúhelníkových parket – konvexní pětiúhelníky, které lze použít k obkládání roviny bez mezer nebo přesahů.